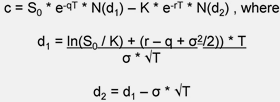Models for FAS 123(R): Lattice vs. Black-ScholesApril 5, 2005, Chicago Consulting Actuaries, LLCThe biggest problem with expensing stock options -- and the main objection of opponents of the revised standard -- is that the value of an option is in some fundamental sense speculative. Exchange-traded options have a value set by a (generally) liquid and transparent market. Participants in options markets have developed a set of tools (valuation formulas) for valuing options which are generally regarded as useful. But employee stock options are not exchange-traded and have a number of features that differ radically from exchange-traded options. Exchange-traded options are generally for a short term (a year or less) and the option holder's ability to exercise is unrestricted during the option term. A typical employee stock option has a term of 10 years. Frequently, it includes a vesting provision -- the option cannot be exercised until the employee has completed, say, three years of service. It will also, typically, have a provision requiring exercise within, say, 90 days of termination of employment. There will also be blackout periods and insider trading restrictions on exercise. These and other features of employee stock options make the valuation of them more complicated than the valuation of exchange traded options. Now, let's turn to a review of different option valuation strategies. Valuation Method AlternativesThe oldest and most famous valuation method is the "Black-Scholes" method. This method uses a differential equation seeded with embedded assumptions. Without going into mathematical detail, by plugging key variables into the Black-Scholes formula -- the price and price-volatility of the underlying stock and the rate of return on a risk free investment (the risk-free interest rate) -- the Black-Scholes formula produces a value for an option. Black-Scholes and Black-Scholes-derived formulas have been effectively used for years in valuing exchange-traded options. And in that context they are generally regarded as theoretically and empirically sound. Black-Scholes works like a black box, or better, a rule of thumb. By plugging a limited set of variables into a differential equation, you can derive a value for an option. A handy thing to have if, for instance, you're trading market-valued options in real time.
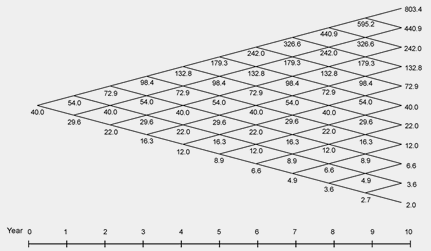
Adapting Black-Scholes to employee options has, however, proved cumbersome. Let's review the problems employee options present. Black-Scholes assumes trading in the underlying stock, and the ability to exercise the option, is continuous and unrestricted. But as already mentioned, employee options are subject to a number of restrictions -- vesting periods, blackouts, and securities law insider trading restrictions. Black-Scholes assumes a constant risk-free interest rate. For a 3 month option such an assumption may be reasonable, but not for the 10 year term typical for employee options. Similarly, Black-Scholes assumes volatility is constant over the option period. Again, a reasonable assumption for three months but not for 10 years. Dividend-paying stocks pose additional complications in setting assumptions for both the risk-free rate and volatility under the model. Black-Scholes assumes a "risk neutral environment" -- you don't have to factor in the risk tolerance of individual option holders. That's a reasonable assumption in a broad and liquid market. There are enough risk-neutral market participants to prevent price anomalies resulting from the risk (or anti-risk) preference of any individual option holder. But in many respects an employee option holder represents a market of one. If the individual employee has a conservative risk preference, he or she may not be able to realize the full value of the option predicted by Black-Scholes's risk-neutral model -- he or she may sell too soon. These Black-Scholes assumptions keep the Black-Scholes formula (relatively) simple. Theoretically, more elaborate formulas could be developed to accommodate each of these variables, but, generally, such formulas would be so awkward and huge as to be unusable. In practice, those who have applied Black-Scholes to employee options have applied "rough answer" rules-of-thumb to discount for, for instance, the effect on value of restrictions on trading. Alternative to Black-Scholes: The Lattice ModelBlack-Scholes was developed before the desktop computer age, when the calculating power available to most market participants was very limited. One rule-of-thumb equation worked nicely for valuations of short term exchange traded options made on the fly. But the subtlety of the calculations needed to accommodate all the factors at work in an employee option simply doesn't fit into Black-Scholes one-master-differential-equation-fits-all methodology. To deal with more complex options, a more flexible valuation methodology was developed known as the lattice model. The lattice model is in concept simpler than Black-Scholes. Starting with similar data about price and similar assumptions about interest and volatility (similar, that is, to the assumptions you would use in applying Black-Scholes) , the lattice model maps a range of results one iteration out, and then one more iteration out, and one more and so on.
If you use the same data about price and make the same assumptions about interest rates and volatility as you do under Black-Scholes, then, using the lattice model, you get the same result as you do under Black-Scholes.
But the lattice model allows you to -- at each iteration -- bake in new assumptions. For instance, let's begin with the kind of assumptions you'd use doing a Black-Scholes valuation --
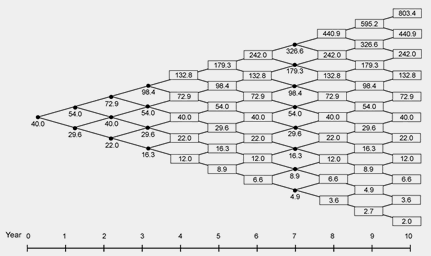
Now let's add some provisions typical of an employee option --
Adding the latter two sets of assumptions into a Black-Scholes derived differential equation is practically impossible. But they map into the lattice seamlessly and intuitively.
So, how does the valuation change as we include features specific to employee options, as well as other valuation assumptions not easily handled by Black-Scholes?
To sum up, the lattice model allows you to use the same assumptions about the relationships between prices, interest rates and volatility that underlie Black-Scholes, while allowing you to add to and elaborate on these variables, using the brute calculating power of modern computers to do the "billions and billions" of calculations required. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
This is a publication of Chicago Consulting Actuaries. If you have any comments or questions, please contact your CCA Consultant or Daniel Cox. The information, analyses and opinions set out herein are for general information only and are not intended to provide specific advice or recommendations for any individual or entity. Nothing herein constitutes or should be construed as a legal opinion or advice. You should consult your own attorney, accountant, financial or tax advisor or other planner or consultant with regard to your own situation or that of any entity which you represent or advise. Information set out or referred to above has been obtained from sources believed to be reliable. However, neither Chicago Consulting Actuaries nor any of its affiliates has verified the accuracy or completeness of any such information. Neither Chicago Consulting Actuaries nor any of its affiliates shall have any liability for any use of the information set out or referred to herein. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||